四国军棋博弈论——四国军棋理论研究的新高度
博弈论求解四国军棋残局实例
弹子认为,四国军棋发展受限的主要原因,在于理论的缺乏。四国军棋必须建立起自己的理论体系,才可能与象棋、围棋争奇斗艳。在多年的研究中,弹子找到了新的工具——博弈论,开创了用博弈论来研究四国军棋的先河。
----------------------------------------------------------------------------------
昨天,接到黄埔MM的@,如下:
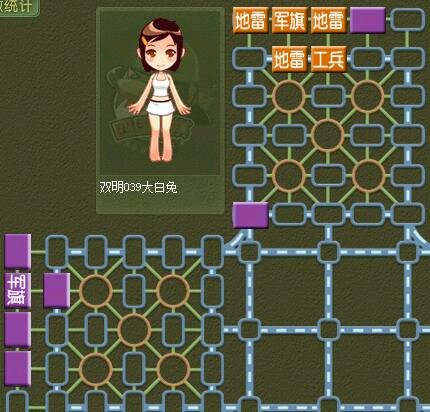
橙色三角雷和工兵已明。紫色没有工兵和炸弹,雷区四个暗棋有三个是雷,橙先。
方案一:橙色游走工兵,选择和棋。
方案二:飞紫色棋上,博取赢棋的可能。
@弹子兵法 你的理论不用十年,一年就可以了,如果一个月可以解开这局。。
----------------------------------------------------------------------------------
昨天,接到黄埔MM的@,如下:
橙色三角雷和工兵已明。紫色没有工兵和炸弹,雷区四个暗棋有三个是雷,橙先。
方案一:橙色游走工兵,选择和棋。
方案二:飞紫色棋上,博取赢棋的可能。
@弹子兵法 你的理论不用十年,一年就可以了,如果一个月可以解开这局。。
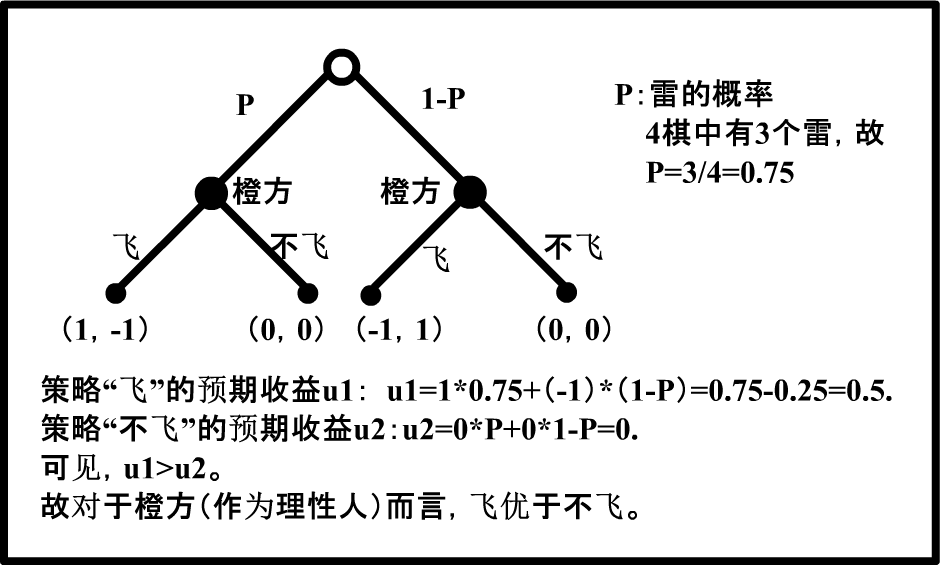
解答:设胜的收益为1,败的收益为-1,和的收益为0。
由题知,敌方旗台为雷的概率为P,且4棋中有3雷,故旗台是雷概率为3/4=0.75。
得到动态博弈树如下:
原贴地址:https://tieba.baidu.com/p/5578260025
简单解释如下:(1)旗台是雷的概率是0.75。这个很容易理解。
(2)由于有两种情况,所以分成两部分来研究其收益,一部分为0.75概率的,一个是0.25概率的。
(3)橙方有两个策略(是雷或不是雷都有这两个策略):飞或不飞,所以分别将它们写出(是雷和非雷),在是雷和不是雷情况下的收益写出来(收益前面一个数字是橙方的,第二个数字是敌方的。本题其实只需要讨论橙方)。
(4)计算比较,得出最优策略:当选择飞时,用其收益乘以概率。在飞的情况下,实际上有两种收益,是雷和不是雷。所以分别用其收益乘以相应概率。于是得到了策略“飞”下的预期收益。(预期收益是博弈论的一个概念)
(5)比较一下预期收益,最大者即为最佳的策略。
如果要问,何时(雷的概率是多少是)该飞,何时不该飞呢?
答:u1=1*P+(-1)*(1-P)=2P-1。令2P=0,(即飞与不飞时预期收益相同),
解得P=0.5,即当P>0.5时,飞;当P<0.5时,不飞。